Part 2: The Structure of Mathematics
You did read Part 1 first, right?
The difference between math and science is that they are not built the same. Science happens because we see that something seems to happen over and over again, and we come up with an explanation for why it happens the way it does. That explanation will ideally then be applicable to other situations. So, we run tests and see if the new situations do indeed act according to the new explanation. Sometimes they do. The standard model of physics has stood up to every situation that humans can think to throw at it. Sometimes they don’t. Newton’s theory of gravitation worked fine for cannon balls and for the moon (at least up to our ability to measure things), but it didn’t work when applied to the orbit of Mercury.
Math doesn’t work like this at all. Math is asking a different question from the start. Math wants to know what things are always true. What things will continue to be true no matter what new discoveries are made?1 This question is much tougher. It is so tough in fact that one cannot really make any progress without having some simple starting point. So, what mathematicians do is pick a few definitions and a few propositions which it seems no one could possibly question and start there. Two-thousand years of geometry was developed on five such assumptions. They are usually called Euclid’s five postulates.2 Here they are paraphrased and updated a little:
- For any two points, one can draw a line going through them.
- One can truncate or extend lines.
- One can create a circle with any center and radius.
- All right angles are equal to one another.
- For any point
 not on a line
not on a line 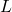 , there is one and only one line that passes through P and does not intersect
, there is one and only one line that passes through P and does not intersect 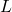 .
.
Having a starting place is good, but it doesn’t help much if you don’t have any way to travel from the starting point. These are usually called Euclid’s axioms, and he had five of these as well:
- Things which are equal to the same thing are also equal to one another.
- If equals be added to equals, the wholes are equal.
- If equals be subtracted from equals, the remainders are equal.
- Things which coincide with one another are equal to one another.
- The whole is greater than the part.
There are definitely some issues here. Euclid never tells us exactly what he means by line or point. He just assumes we know. The fifth postulate is a mess (see the footnote above), and the fourth axiom could use a little clarification, but on the whole, these seem like a good starting place.
The whole idea here is that if we find a starting place that can’t possibly be false and then only makes moves that lead us to other true positions, then we can develop a set of ideas that are definitely true. The key word here is definitely. Newton’s laws seemed to work, but there was nothing demanding that they actually were the laws of our universe. They just fit the data (until they didn’t anymore). The standard model seems to fit the data today, but we have no way of knowing for sure if it’s really true or just a really good approximation in almost all situations.
Math wants to do something else. Math wants to find things that are guaranteed to always be true. It wants to find the things that are true not just because the universe works a certain way, but because logic and Truth itself demands it. So, it starts with a few simple nuggets of truth and a few simple methods of obtaining new truths and starts building from there.
You can imagine Euclid’s geometry as a labyrinthine cave of true things. The postulates and axioms are like the entrance and main chamber. Each new major fact discovered is like a new room in the cave and the proof of that fact is like a hallway that leads to the room. From these rooms new hallways and rooms branch off. They break off and they weave back together creating a great web. The rooms often have secrets and tools that we can then use to find new paths and open secret doors. And there are monsters too, and they block your path. Sometimes you slay them and continue down the hallway to the next room without much trouble. But sometimes the monsters are large and no one knows how to defeat them yet. And mathematicians keep exploring hoping some new room will have some magical item that will let them defeat the monster and continue on. And no one knows if some of the monsters are invulnerable or not.
Each field of math is like one of these caves. Each has its own starting assumptions and its own methods and techniques for finding new rooms, and each cave seems to stand on its own. Yet, there are relationships between the caves themselves, and mathematicians have found ways to teleport back and forth between them in ways that also lead to new truths. When they teleport back, they sometimes end up in new rooms entirely, and they then know there must be a path to get there, but they have no way to find it. They search for some source of light to illuminate some secret passage hidden in the darkness. And the whole thing keeps growing in complexity as more and more people take off into the darkness mapping things as they go.
No one really knows for sure why, but the cave systems are full of items and tools that give us magical powers in the real world. It is just barely an exaggeration to say that all of our science and technology have come from people exploring the caves. And this leads to one of the problems with math classes. For the most part, in a math class you are just shown pictures of the rooms in the caves or shown a couple of the items that we found there. If your teacher is particularly enthusiastic, they will say “Look how beautiful it is. Look at this thing we found. Look what we can do with it!”, and that is all well and good. To some degree it has to work that way. Most students are taking a Calculus class, say, because they need the Calculus for a specific reason. Maybe they are looking to become physicists and they need the Calculus specifically to start learning their physics. So, instead of exploring the caves, they are shown a photo album of the most beautiful and most useful rooms and that is that.
Make no mistake, mathematicians like looking at these photo albums as well. They like showing them to people, and they like playing with the tools and toys that have been found. They are beautiful and fun, and these albums serve as a showcase and reminder of everything that we have found so far, but they are no substitute for exploring the cave system yourself, even if only to walk the paths that others have already plotted. Who knows? You may find a hidden hallway hiding in the shadows somewhere that no one has seen before.
So, that is what I want to do. I want to do a bit of exploring together. Just a little bit. But the cave systems are so vast and complex that it doesn’t hurt to have a strategy guide, and that is what I hope this series to be: a quick start guide for exploration. So, let us start to explore these realms together. It is an overwhelming place at first, but we will learn to embrace the magnitude of it all as we go.
Part 3 coming soon …
Footnotes
- Most mathematicians actually use the term Pure Mathematics for what I am describing. There is another side to Math called Applied Mathematics which seeks to apply and develop mathematics specifically for scientific (and other) situations. For the sake of simplification, I am going to just use the term Mathematics here. ↩︎
- Entire books have been written about these postulates, in particular the fifth one, which feels, let us say, not as obvious as the others. ↩︎
